|
Clinician's corner |
|
Back to main page |
|
Programmer's corner |
| So, you use WinBUGS a lot? Want more? |
|
Patrick Blisle Division of Clinical Epidemiology McGill University Health Center Montreal, Quebec CANADA patrick.belisle@rimuhc.ca Last modification: 7 feb 2017
|
|
|
Version 1.3 (February 2017)
beta.parms.from.quantiles
[R] Computing Beta distribution parameters
| [ | beta.parms.from.quantiles is an R function developped to compute Beta distribution parameters fitting specified quantiles and cumulative probabilities. | ] |
Menu
Top
Syntax
beta.parms.from.quantiles <- function(q, p=c(0.025,0.975), precision=0.001, derivative.epsilon=1e-3, start.with.normal.approx=T, start=c(1,1), plot=F)
Top
beta.parms.from.quantiles arguments
| Argument | Value | Comment |
| q | Vector of quantiles; | Vector of length 2; |
| p | Vector of probabilities; |
Vector of length 2. Default is (0.025, 0.975). |
| precision | Desired precision in Beta distribution parameters; | The algoritm in beta.parms.from.quantiles is iterative: it will stop when an iteration leads to (a, b) estimates that do not differ from estimates obtained in last iteration by more than precision. |
| derivative.epsilon | Small value used for ε in the approximation of the derivatives of a few functions in the algorithm; | A few functions (f) have derivates (f'(x)) that are approximated by (f(x+ε)) - f(x))/ε) in the algorithm, where ε = derivative.epsilon. If the algorithm fails to return correct Beta distribution parameters, you may want to try again with smaller values than the default (1e-3) for this parameter. |
| start.with.normal.approx | Logical. Whether or not to start the iterative process with values obtained from a normal approximation to the Beta distribution; | Default is T. |
| start | Vector (of length 2) of initial values for Beta distribution parameters. | Ignored when start.with.normal.approx is True. |
| plot | Logical. Whether or not to plot the resulting Beta distribution, along with tail probabilities obtained. | Default is F. |
Top
Output
| Output dimension | Value |
| $a $b |
parameters of the Beta distribution; |
| $last.change | last change in $a and $b in the iterative algorithm; |
| $niter | number of iterations run before convergence; |
| $q | quantiles; |
| $p | probabilities; |
| $p.check | a quick validation: values for $a and $b returned lead to cumulative probabilities $p.check at the quantiles $q. |
Top
Example
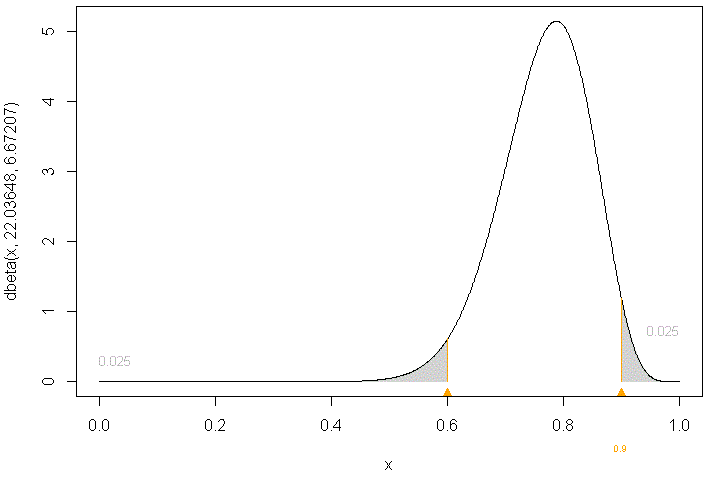
The code below reproduces the input and output of an R session involving a call to beta.parms.from.quantiles. The use of option plot=T produces the plot attached below (default is to not produce the plot).
The output shows that a Beta distribution with shape parameters α=22.04 and β=6.67 lies in range (0.6, 0.9) with probability 95%, with equal probability tails.
> source('c:/path/BetaParmsFromQuantiles.R') # load file where beta.parms.from.quantiles R function is defined
> beta.parms.from.quantiles(c(.6,.9), plot=T)
> beta.parms.from.quantiles(c(.6,.9), plot=T)
|
$a [1] 22.03648 $b [1] 6.672066 $last.change [1] -6.551463e-05 -2.695784e-05 $niter [1] 5 $q [1] 0.6 0.9 $p [1] 0.025 0.975 $p.check [1] 0.025 0.975 |
|
Use in a Bayesian context
Beta densities are frequently used as prior distributions in Bayesian analysis, as they are the conjugate density to binomial likelihoods. Many parameters whose range is the interval [0,1], for example, the prevalence of a disease or the sensitivity and specificity of a diagnostic test, can be modeled with a binomial likelihood function, and hence are conveniently given Beta prior densities.
To illustrate, suppose the prior range of a given parameter is (0.6, 0.9) with probability 95%, then its prior density could be a Beta distribution with parameters α=22.04 and β=6.67, as per above beta.parms.from.quantiles results.
Top
Code
beta.parms.from.quantiles <- function(q, p=c(0.025,0.975),
precision=0.001, derivative.epsilon=1e-3, start.with.normal.approx=T, start=c(1, 1), plot=F)
{
# Version 1.3 (February 2017)
#
# Function developed by
# Lawrence Joseph and pbelisle
# Division of Clinical Epidemiology
# Montreal General Hospital
# Montreal, Qc, Can
#
# patrick.belisle@rimuhc.ca
# http://www.medicine.mcgill.ca/epidemiology/Joseph/PBelisle/BetaParmsFromQuantiles.html
#
# Please refer to our webpage for details on each argument.
f <- function(x, theta){dbeta(x, shape1=theta[1], shape2=theta[2])}
F.inv <- function(x, theta){qbeta(x, shape1=theta[1], shape2=theta[2])}
f.cum <- function(x, theta){pbeta(x, shape1=theta[1], shape2=theta[2])}
f.mode <- function(theta){a <- theta[1]; b <- theta[2]; mode <- ifelse(a>1, (a-1)/(a+b-2), NA); mode}
theta.from.moments <- function(m, v){a <- m*m*(1-m)/v-m; b <- a*(1/m-1); c(a, b)}
plot.xlim <- c(0, 1)
dens.label <- 'dbeta'
parms.names <- c('a', 'b')
if (length(p) != 2) stop("Vector of probabilities p must be of length 2.")
if (length(q) != 2) stop("Vector of quantiles q must be of length 2.")
p <- sort(p); q <- sort(q)
#_____________________________________________________________________________________________________
print.area.text <- function(p, p.check, q, f, f.cum, F.inv, theta, mode, cex, plot.xlim, M=30, M0=50)
{
par.usr <- par('usr')
par.din <- par('din')
p.string <- as.character(round(c(0,1) + c(1,-1)*p.check, digits=4))
str.width <- strwidth(p.string, cex=cex)
str.height <- strheight("0", cex=cex)
J <- matrix(1, nrow=M0, ncol=1)
x.units.1in <- diff(par.usr[c(1,2)])/par.din[1]
y.units.1in <- diff(par.usr[c(3,4)])/par.din[2]
aspect.ratio <- y.units.1in/x.units.1in
# --- left area -----------------------------------------------------------
scatter.xlim <- c(max(plot.xlim[1], par.usr[1]), q[1])
scatter.ylim <- c(0, par.usr[4])
x <- seq(from=scatter.xlim[1], to=scatter.xlim[2], length=M)
y <- seq(from=scatter.ylim[1], to=scatter.ylim[2], length=M)
x.grid.index <- rep(seq(M), M)
y.grid.index <- rep(seq(M), rep(M, M))
grid.df <- f(x, theta)
# Estimate mass center
tmp.p <- seq(from=0, to=p[1], length=M0)
tmp.x <- F.inv(tmp.p, theta)
h <- f(tmp.x, theta)
mass.center <- c(mean(tmp.x), sum(h[-1]*diff(tmp.x))/diff(range(tmp.x)))
# Identify points under the curve
# (to eliminate them from the list of candidates)
gridpoint.under.the.curve <- y[y.grid.index] <= grid.df[x.grid.index]
w <- which(gridpoint.under.the.curve)
x <- x[x.grid.index]; y <- y[y.grid.index]
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points to the right of the mode, if any
w <- which(x>mode)
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points for which the text would fall out of the plot area
w <- which((par.usr[1]+str.width[1]) <= x & (y + str.height) <= par.usr[4])
x <- x[w]; y <- y[w]
# For each height, eliminate the closest point to the curve
# (we want to stay away from the curve to preserve readability)
w <- which(!duplicated(y, fromLast=T))
if (length(w)){x <- x[-w]; y <- y[-w]}
# For each point, compute distance from mass center and pick the closest point
d <- ((x-mass.center[1])^2) + ((y-mass.center[2])/aspect.ratio)^2
w <- which.min(d)
x <- x[w]; y <- y[w]
if (length(x))
{
text(x, y, labels=p.string[1], adj=c(1,0), col='gray', cex=cex)
}
else
{
text(plot.xlim[1], mean(par.usr[c(3,4)]), labels=p.string[1], col='gray', cex=cex, srt=90, adj=c(1,0))
}
# --- right area ----------------------------------------------------------
scatter.xlim <- c(q[2], plot.xlim[2])
scatter.ylim <- c(0, par.usr[4])
x <- seq(from=scatter.xlim[1], to=scatter.xlim[2], length=M)
y <- seq(from=scatter.ylim[1], to=scatter.ylim[2], length=M)
x.grid.index <- rep(seq(M), M)
y.grid.index <- rep(seq(M), rep(M, M))
grid.df <- f(x, theta)
# Estimate mass center
tmp.p <- seq(from=p[2], to=f.cum(plot.xlim[2], theta), length=M0)
tmp.x <- F.inv(tmp.p, theta)
h <- f(tmp.x, theta)
mass.center <- c(mean(tmp.x), sum(h[-length(h)]*diff(tmp.x))/diff(range(tmp.x)))
# Identify points under the curve
# (to eliminate them from the list of candidates)
gridpoint.under.the.curve <- y[y.grid.index] <= grid.df[x.grid.index]
w <- which(gridpoint.under.the.curve)
x <- x[x.grid.index]; y <- y[y.grid.index]
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points to the left of the mode, if any
w <- which(x
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points for which the text would fall out of the plot area
w <- which((par.usr[2]-str.width[2]) >= x & (y + str.height) <= par.usr[4])
x <- x[w]; y <- y[w]
# For each height, eliminate the closest point to the curve
# (we want to stay away from the curve to preserve readability)
w <- which(!duplicated(y))
if (length(w)){x <- x[-w]; y <- y[-w]}
# For each point, compute distance from mass center and pick the closest point
d <- ((x-mass.center[1])^2) + ((y-mass.center[2])/aspect.ratio)^2
w <- which.min(d)
x <- x[w]; y <- y[w]
if (length(x))
{
text(x, y, labels=p.string[2], adj=c(0,0), col='gray', cex=cex)
}
else
{
text(plot.xlim[2], mean(par.usr[c(3,4)]), labels=p.string[2], col='gray', cex=cex, srt=-90, adj=c(1,0))
}
}
# ......................................................................................................................................
Newton.Raphson <- function(derivative.epsilon, precision, f.cum, p, q, theta.from.moments, start.with.normal.approx, start)
{
Hessian <- matrix(NA, 2, 2)
if (start.with.normal.approx)
{
# Probably not a very good universal choice, but proved good in most cases in practice
m <- diff(q)/diff(p)*(0.5-p[1]) + q[1]
v <- (diff(q)/diff(qnorm(p)))^2
theta <- theta.from.moments(m, v)
}
else theta <- start
change <- precision + 1
niter <- 0
# Newton-Raphson multivariate algorithm
while (max(abs(change)) > precision)
{
Hessian[,1] <- (f.cum(q, theta) - f.cum(q, theta - c(derivative.epsilon, 0))) / derivative.epsilon
Hessian[,2] <- (f.cum(q, theta) - f.cum(q, theta - c(0, derivative.epsilon))) / derivative.epsilon
f <- f.cum(q, theta) - p
change <- solve(Hessian) %*% f
last.theta <- theta
theta <- last.theta - change
# If we step out of limits, reduce change
if (any(theta<0))
{
w <- which(theta<0)
k <- min(last.theta[w]/change[w])
theta <- last.theta - k/2*change
}
niter <- niter + 1
}
list(theta=as.vector(theta), niter=niter, last.change=as.vector(change))
}
# ...............................................................................................................
plot.density <- function(p, q, f, f.cum, F.inv, mode, theta, plot.xlim, dens.label, parms.names, cex)
{
if (length(plot.xlim) == 0)
{
plot.xlim <- F.inv(c(0, 1), theta)
if (is.infinite(plot.xlim[1]))
{
tmp <- min(c(0.001, p[1]/10))
plot.xlim[1] <- F.inv(tmp, theta)
}
if (is.infinite(plot.xlim[2]))
{
tmp <- max(c(0.999, 1 - (1-p[2])/10))
plot.xlim[2] <- F.inv(tmp, theta)
}
}
plot.xlim <- sort(plot.xlim)
x <- seq(from=min(plot.xlim), to=max(plot.xlim), length=1000)
h <- f(x, theta)
x0 <- x; f0 <- h
ylab <- paste(c(dens.label, '(x, ', parms.names[1], ' = ', round(theta[1], digits=5), ', ', parms.names[2], ' = ', round(theta[2], digits=5), ')'), collapse='')
plot(x, h, type='l', ylab=ylab)
# fill in area on the left side of the distribution
x <- seq(from=plot.xlim[1], to=q[1], length=1000)
y <- f(x, theta)
x <- c(x, q[1], plot.xlim[1]); y <- c(y, 0, 0)
polygon(x, y, col='lightgrey', border='lightgray')
# fill in area on the right side of the distribution
x <- seq(from=max(plot.xlim), to=q[2], length=1000)
y <- f(x, theta)
x <- c(x, q[2], plot.xlim[2]); y <- c(y, 0, 0)
polygon(x, y, col='lightgrey', border='lightgray')
# draw distrn again
points(x0, f0, type='l')
h <- f(q, theta)
points(rep(q[1], 2), c(0, h[1]), type='l', col='orange')
points(rep(q[2], 2), c(0, h[2]), type='l', col='orange')
# place text on both ends areas
print.area.text(p, p.check, q, f, f.cum, F.inv, theta, mode, cex, plot.xlim)
xaxp <- par("xaxp")
x.ticks <- seq(from=xaxp[1], to=xaxp[2], length=xaxp[3]+1)
q2print <- as.double(setdiff(as.character(q), as.character(x.ticks)))
mtext(q2print, side=1, col='orange', at=q2print, cex=0.6, line=2.1)
points(q, rep(par('usr')[3]+0.15*par('cxy')[2], 2), pch=17, col='orange')
}
#________________________________________________________________________________________________________________
parms <- Newton.Raphson(derivative.epsilon, precision, f.cum, p, q, theta.from.moments, start.with.normal.approx, start=start)
p.check <- f.cum(q, parms$theta)
if (plot) plot.density(p, q, f, f.cum, F.inv, f.mode(parms$theta), parms$theta, plot.xlim, dens.label, parms.names, 0.8)
list(a=parms$theta[1], b=parms$theta[2], last.change=parms$last.change, niter=parms$niter, q=q, p=p, p.check=p.check)
}
precision=0.001, derivative.epsilon=1e-3, start.with.normal.approx=T, start=c(1, 1), plot=F)
{
# Version 1.3 (February 2017)
#
# Function developed by
# Lawrence Joseph and pbelisle
# Division of Clinical Epidemiology
# Montreal General Hospital
# Montreal, Qc, Can
#
# patrick.belisle@rimuhc.ca
# http://www.medicine.mcgill.ca/epidemiology/Joseph/PBelisle/BetaParmsFromQuantiles.html
#
# Please refer to our webpage for details on each argument.
f <- function(x, theta){dbeta(x, shape1=theta[1], shape2=theta[2])}
F.inv <- function(x, theta){qbeta(x, shape1=theta[1], shape2=theta[2])}
f.cum <- function(x, theta){pbeta(x, shape1=theta[1], shape2=theta[2])}
f.mode <- function(theta){a <- theta[1]; b <- theta[2]; mode <- ifelse(a>1, (a-1)/(a+b-2), NA); mode}
theta.from.moments <- function(m, v){a <- m*m*(1-m)/v-m; b <- a*(1/m-1); c(a, b)}
plot.xlim <- c(0, 1)
dens.label <- 'dbeta'
parms.names <- c('a', 'b')
if (length(p) != 2) stop("Vector of probabilities p must be of length 2.")
if (length(q) != 2) stop("Vector of quantiles q must be of length 2.")
p <- sort(p); q <- sort(q)
#_____________________________________________________________________________________________________
print.area.text <- function(p, p.check, q, f, f.cum, F.inv, theta, mode, cex, plot.xlim, M=30, M0=50)
{
par.usr <- par('usr')
par.din <- par('din')
p.string <- as.character(round(c(0,1) + c(1,-1)*p.check, digits=4))
str.width <- strwidth(p.string, cex=cex)
str.height <- strheight("0", cex=cex)
J <- matrix(1, nrow=M0, ncol=1)
x.units.1in <- diff(par.usr[c(1,2)])/par.din[1]
y.units.1in <- diff(par.usr[c(3,4)])/par.din[2]
aspect.ratio <- y.units.1in/x.units.1in
# --- left area -----------------------------------------------------------
scatter.xlim <- c(max(plot.xlim[1], par.usr[1]), q[1])
scatter.ylim <- c(0, par.usr[4])
x <- seq(from=scatter.xlim[1], to=scatter.xlim[2], length=M)
y <- seq(from=scatter.ylim[1], to=scatter.ylim[2], length=M)
x.grid.index <- rep(seq(M), M)
y.grid.index <- rep(seq(M), rep(M, M))
grid.df <- f(x, theta)
# Estimate mass center
tmp.p <- seq(from=0, to=p[1], length=M0)
tmp.x <- F.inv(tmp.p, theta)
h <- f(tmp.x, theta)
mass.center <- c(mean(tmp.x), sum(h[-1]*diff(tmp.x))/diff(range(tmp.x)))
# Identify points under the curve
# (to eliminate them from the list of candidates)
gridpoint.under.the.curve <- y[y.grid.index] <= grid.df[x.grid.index]
w <- which(gridpoint.under.the.curve)
x <- x[x.grid.index]; y <- y[y.grid.index]
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points to the right of the mode, if any
w <- which(x>mode)
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points for which the text would fall out of the plot area
w <- which((par.usr[1]+str.width[1]) <= x & (y + str.height) <= par.usr[4])
x <- x[w]; y <- y[w]
# For each height, eliminate the closest point to the curve
# (we want to stay away from the curve to preserve readability)
w <- which(!duplicated(y, fromLast=T))
if (length(w)){x <- x[-w]; y <- y[-w]}
# For each point, compute distance from mass center and pick the closest point
d <- ((x-mass.center[1])^2) + ((y-mass.center[2])/aspect.ratio)^2
w <- which.min(d)
x <- x[w]; y <- y[w]
if (length(x))
{
text(x, y, labels=p.string[1], adj=c(1,0), col='gray', cex=cex)
}
else
{
text(plot.xlim[1], mean(par.usr[c(3,4)]), labels=p.string[1], col='gray', cex=cex, srt=90, adj=c(1,0))
}
# --- right area ----------------------------------------------------------
scatter.xlim <- c(q[2], plot.xlim[2])
scatter.ylim <- c(0, par.usr[4])
x <- seq(from=scatter.xlim[1], to=scatter.xlim[2], length=M)
y <- seq(from=scatter.ylim[1], to=scatter.ylim[2], length=M)
x.grid.index <- rep(seq(M), M)
y.grid.index <- rep(seq(M), rep(M, M))
grid.df <- f(x, theta)
# Estimate mass center
tmp.p <- seq(from=p[2], to=f.cum(plot.xlim[2], theta), length=M0)
tmp.x <- F.inv(tmp.p, theta)
h <- f(tmp.x, theta)
mass.center <- c(mean(tmp.x), sum(h[-length(h)]*diff(tmp.x))/diff(range(tmp.x)))
# Identify points under the curve
# (to eliminate them from the list of candidates)
gridpoint.under.the.curve <- y[y.grid.index] <= grid.df[x.grid.index]
w <- which(gridpoint.under.the.curve)
x <- x[x.grid.index]; y <- y[y.grid.index]
if (length(w)){x <- x[-w]; y <- y[-w]}
# Eliminate points to the left of the mode, if any
w <- which(x
# Eliminate points for which the text would fall out of the plot area
w <- which((par.usr[2]-str.width[2]) >= x & (y + str.height) <= par.usr[4])
x <- x[w]; y <- y[w]
# For each height, eliminate the closest point to the curve
# (we want to stay away from the curve to preserve readability)
w <- which(!duplicated(y))
if (length(w)){x <- x[-w]; y <- y[-w]}
# For each point, compute distance from mass center and pick the closest point
d <- ((x-mass.center[1])^2) + ((y-mass.center[2])/aspect.ratio)^2
w <- which.min(d)
x <- x[w]; y <- y[w]
if (length(x))
{
text(x, y, labels=p.string[2], adj=c(0,0), col='gray', cex=cex)
}
else
{
text(plot.xlim[2], mean(par.usr[c(3,4)]), labels=p.string[2], col='gray', cex=cex, srt=-90, adj=c(1,0))
}
}
# ......................................................................................................................................
Newton.Raphson <- function(derivative.epsilon, precision, f.cum, p, q, theta.from.moments, start.with.normal.approx, start)
{
Hessian <- matrix(NA, 2, 2)
if (start.with.normal.approx)
{
# Probably not a very good universal choice, but proved good in most cases in practice
m <- diff(q)/diff(p)*(0.5-p[1]) + q[1]
v <- (diff(q)/diff(qnorm(p)))^2
theta <- theta.from.moments(m, v)
}
else theta <- start
change <- precision + 1
niter <- 0
# Newton-Raphson multivariate algorithm
while (max(abs(change)) > precision)
{
Hessian[,1] <- (f.cum(q, theta) - f.cum(q, theta - c(derivative.epsilon, 0))) / derivative.epsilon
Hessian[,2] <- (f.cum(q, theta) - f.cum(q, theta - c(0, derivative.epsilon))) / derivative.epsilon
f <- f.cum(q, theta) - p
change <- solve(Hessian) %*% f
last.theta <- theta
theta <- last.theta - change
# If we step out of limits, reduce change
if (any(theta<0))
{
w <- which(theta<0)
k <- min(last.theta[w]/change[w])
theta <- last.theta - k/2*change
}
niter <- niter + 1
}
list(theta=as.vector(theta), niter=niter, last.change=as.vector(change))
}
# ...............................................................................................................
plot.density <- function(p, q, f, f.cum, F.inv, mode, theta, plot.xlim, dens.label, parms.names, cex)
{
if (length(plot.xlim) == 0)
{
plot.xlim <- F.inv(c(0, 1), theta)
if (is.infinite(plot.xlim[1]))
{
tmp <- min(c(0.001, p[1]/10))
plot.xlim[1] <- F.inv(tmp, theta)
}
if (is.infinite(plot.xlim[2]))
{
tmp <- max(c(0.999, 1 - (1-p[2])/10))
plot.xlim[2] <- F.inv(tmp, theta)
}
}
plot.xlim <- sort(plot.xlim)
x <- seq(from=min(plot.xlim), to=max(plot.xlim), length=1000)
h <- f(x, theta)
x0 <- x; f0 <- h
ylab <- paste(c(dens.label, '(x, ', parms.names[1], ' = ', round(theta[1], digits=5), ', ', parms.names[2], ' = ', round(theta[2], digits=5), ')'), collapse='')
plot(x, h, type='l', ylab=ylab)
# fill in area on the left side of the distribution
x <- seq(from=plot.xlim[1], to=q[1], length=1000)
y <- f(x, theta)
x <- c(x, q[1], plot.xlim[1]); y <- c(y, 0, 0)
polygon(x, y, col='lightgrey', border='lightgray')
# fill in area on the right side of the distribution
x <- seq(from=max(plot.xlim), to=q[2], length=1000)
y <- f(x, theta)
x <- c(x, q[2], plot.xlim[2]); y <- c(y, 0, 0)
polygon(x, y, col='lightgrey', border='lightgray')
# draw distrn again
points(x0, f0, type='l')
h <- f(q, theta)
points(rep(q[1], 2), c(0, h[1]), type='l', col='orange')
points(rep(q[2], 2), c(0, h[2]), type='l', col='orange')
# place text on both ends areas
print.area.text(p, p.check, q, f, f.cum, F.inv, theta, mode, cex, plot.xlim)
xaxp <- par("xaxp")
x.ticks <- seq(from=xaxp[1], to=xaxp[2], length=xaxp[3]+1)
q2print <- as.double(setdiff(as.character(q), as.character(x.ticks)))
mtext(q2print, side=1, col='orange', at=q2print, cex=0.6, line=2.1)
points(q, rep(par('usr')[3]+0.15*par('cxy')[2], 2), pch=17, col='orange')
}
#________________________________________________________________________________________________________________
parms <- Newton.Raphson(derivative.epsilon, precision, f.cum, p, q, theta.from.moments, start.with.normal.approx, start=start)
p.check <- f.cum(q, parms$theta)
if (plot) plot.density(p, q, f, f.cum, F.inv, f.mode(parms$theta), parms$theta, plot.xlim, dens.label, parms.names, 0.8)
list(a=parms$theta[1], b=parms$theta[2], last.change=parms$last.change, niter=parms$niter, q=q, p=p, p.check=p.check)
}
Top
Download
beta.parms.from.quantiles is a free R function. Download version 1.3 now.
Top
See also
See also gamma.parms.from.quantiles, an R function developped to compute Gamma distribution parameters fitting specified quantiles and cumulative probabilities.