|
Biomedical Signals Acquisition |
Filtering |
| |
There are basically two ways of filtering or
altering the frequency composition of the signal. After applying the
hardware filter to a given signal, the filtered out frequencies from
the signal cannot be recovered. A digital filter changes the
frequency content of a signal by performing calculations on the data:
the filtered frequencies can be recovered once the digital filter is
taken out. |
|
|
|
| Hardware filtering |
|
 |
| From the input
amplifier, one can choose the hardware filter to alter the incoming
signal, with the following results: |
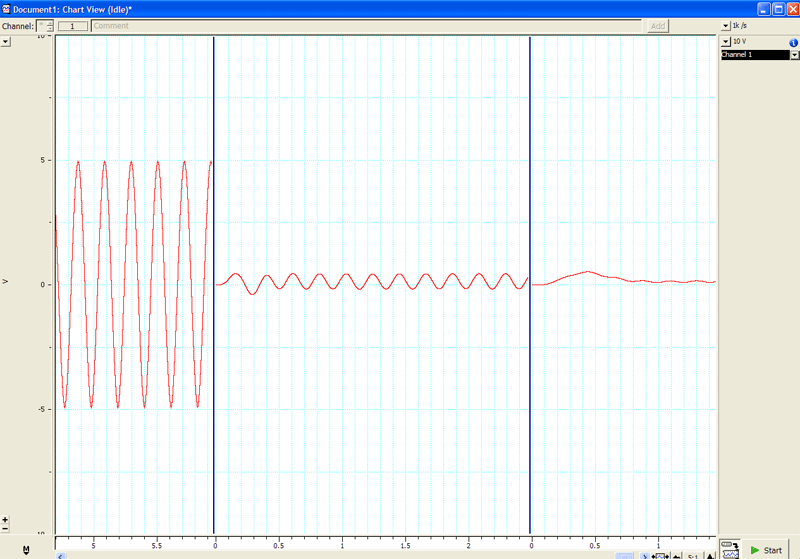 |
|
Left: a 5 Hz sine wave is
acquired, with no low-pass applied.
Middle: a 2 Hz low-pass is applied to the signal.
Right: a 5Hz low-pass is applied to the sine wave. |
|
Ideal versus non-ideal filters |
|
An ideal low-pass filter completely
eliminates all frequencies above the cut-off frequency (=transition
frequency at which the filter takes effect) while passing
those below, unchanged. How is it done? by reducing the amplitude of
frequency signals above the cut-off frequency. An ideal filter provides
a very sharp transition between the frequencies that are passed and
those that are filtered out.This in practice cannot be achieved.
A non-ideal low-pass filter passes low-frequency
signals but attenuates (reduces the amplitude of) signals with
frequencies higher than the cut-off frequencies. |
|
One can plot the amplitude response of a low
pass filter versus the frequencies of signals and obtain the following
curve: |
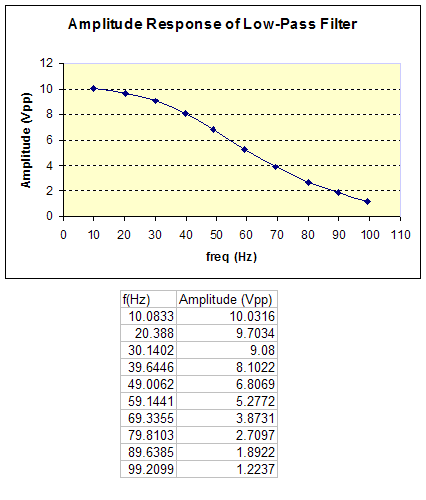 |
- Settings on the data acquisition
system:
The hardware filter (low-pass) was set
to 50 Hz during the entire recording.
- Settings on the waveform
generator:
| waveform
characteristics: |
sine waves |
|
frequency |
10 fold increments
from: 10 Hz to 100 Hz |
|
amplitude |
constant 10 V peak to
peak |
Click here to
view a Flash movie showing the non-ideal filter behaviour |
|
Click here to view a Flash movie and a quiz |
|
Click here to continue with the
next topic, Sampling rate and Aliasing |
|
|
|
|