|
Clinician's corner |
|
Back to main page |
|
Programmer's corner |
| So, you use WinBUGS a lot? Want more? |
|
Patrick Blisle Division of Clinical Epidemiology McGill University Health Center Montreal, Quebec CANADA patrick.belisle@rimuhc.ca Last modification: 28 mar 2012
|
|
|
Version 1.8 (July 2015)
WinBUGSlogs2HtmlSummary
Summarizing WinBUGS output files into an html table
| [ | WinBUGSLogs2htmlSummary is a Perl program to write easy-to-read summaries of Node Statistics found in a series of WinBUGS text log files. | ] |
When running WinBUGS programs, one often runs the same program several times but with small variations, such as trying out different initial values, different prior distributions, or different data sets. Following these runs, one would usually want to compare the results across runs, contained in several distinct WinBUGS log files.
It is not convenient to compare results saved in different WinBUGS log files, so some file manipulations, either on screen or on hard printed copies, are required. The program described on this page, called WinBUGSLogs2HtmlSummary, makes such comparisons easy with only a few mouse clicks. WinBUGSLogs2HtmlSummary is both easy to install and easy to use.
Once it is installed and a shortcut to it has been placed on Desktop, you simply drag-n-drop the WinBUGS text log files to compare onto WinBUGSLogs2HtmlSummary's Desktop Icon and a pop-up form allows you to select nodes to include in summary, change output file name, enter a relevant title, select output maximum width, etc.
Menu
Top
Example
To illustrate the use of WinBUGSLogs2HtmlSummary, we will use the rats example found in WinBUGS documentation, version 1.4.1. The models, data, and inits files are given at the bottom of this page. Suppose for the moment that you have run the two different models presented therein and saved the results to two WinBUGS text log files, named respectively dGammaPrecision-WinBUGSlog.txt and UniformSD-WinBUGSlog.txt, from which the Node statistics are reproduced below, in order.
Node statistics node mean sd MC error 2.5% median 97.5% start sample alpha[1] 239.9 2.671 0.02855 234.7 239.8 245.2 1001 10000 alpha[2] 247.8 2.642 0.02543 242.6 247.8 253.0 1001 10000 alpha[3] 252.4 2.677 0.02487 247.2 252.4 257.6 1001 10000 alpha[4] 232.6 2.671 0.02729 227.3 232.6 237.8 1001 10000 alpha[5] 231.6 2.677 0.02386 226.3 231.6 236.9 1001 10000 alpha[6] 249.7 2.673 0.02963 244.4 249.8 255.0 1001 10000 alpha[7] 228.7 2.647 0.02826 223.6 228.7 233.9 1001 10000 alpha[8] 248.3 2.702 0.02836 243.1 248.4 253.6 1001 10000 alpha[9] 283.3 2.704 0.02751 277.9 283.3 288.6 1001 10000 alpha[10] 219.3 2.692 0.02606 214.1 219.3 224.6 1001 10000 alpha[11] 258.2 2.677 0.02809 253.1 258.2 263.5 1001 10000 alpha[12] 228.1 2.692 0.02707 223.0 228.2 233.4 1001 10000 alpha[13] 242.4 2.693 0.02687 237.2 242.4 247.8 1001 10000 alpha[14] 268.3 2.678 0.02649 263.0 268.3 273.5 1001 10000 alpha[15] 242.8 2.651 0.02715 237.6 242.7 248.1 1001 10000 alpha[16] 245.3 2.682 0.0246 240.1 245.3 250.6 1001 10000 alpha[17] 232.2 2.679 0.02503 226.9 232.2 237.5 1001 10000 alpha[18] 240.5 2.672 0.02549 235.2 240.5 245.7 1001 10000 alpha[19] 253.8 2.686 0.02272 248.5 253.8 259.1 1001 10000 alpha[20] 241.6 2.698 0.02646 236.3 241.6 246.9 1001 10000 alpha[21] 248.6 2.702 0.02906 243.2 248.6 253.8 1001 10000 alpha[22] 225.3 2.684 0.02668 220.0 225.3 230.5 1001 10000 alpha[23] 228.5 2.678 0.02701 223.2 228.5 233.8 1001 10000 alpha[24] 245.1 2.683 0.03076 239.9 245.1 250.4 1001 10000 alpha[25] 234.5 2.715 0.03038 229.2 234.5 239.8 1001 10000 alpha[26] 254.0 2.685 0.02873 248.8 254.0 259.3 1001 10000 alpha[27] 254.4 2.643 0.02636 249.2 254.4 259.5 1001 10000 alpha[28] 243.0 2.692 0.02858 237.7 243.0 248.3 1001 10000 alpha[29] 217.9 2.704 0.02519 212.6 217.9 223.2 1001 10000 alpha[30] 241.4 2.679 0.02763 236.2 241.4 246.8 1001 10000 alpha.c 242.6 2.776 0.02659 237.1 242.6 248.2 1001 10000 alpha0 106.6 3.655 0.04103 99.44 106.5 113.8 1001 10000 beta[1] 6.064 0.2487 0.002582 5.578 6.066 6.555 1001 10000 beta[2] 7.047 0.2532 0.003249 6.542 7.044 7.545 1001 10000 beta[3] 6.483 0.2427 0.002361 6.01 6.482 6.956 1001 10000 beta[4] 5.344 0.2545 0.003057 4.85 5.342 5.838 1001 10000 beta[5] 6.565 0.2462 0.002938 6.085 6.564 7.048 1001 10000 beta[6] 6.172 0.2407 0.002519 5.71 6.172 6.651 1001 10000 beta[7] 5.978 0.2433 0.002409 5.507 5.979 6.449 1001 10000 beta[8] 6.415 0.2471 0.002459 5.937 6.415 6.898 1001 10000 beta[9] 7.047 0.2536 0.003015 6.543 7.053 7.534 1001 10000 beta[10] 5.846 0.2453 0.002693 5.363 5.845 6.327 1001 10000 beta[11] 6.798 0.2493 0.002834 6.304 6.799 7.278 1001 10000 beta[12] 6.121 0.2395 0.002743 5.647 6.12 6.595 1001 10000 beta[13] 6.166 0.2405 0.002348 5.686 6.169 6.635 1001 10000 beta[14] 6.685 0.2452 0.002731 6.202 6.685 7.163 1001 10000 beta[15] 5.416 0.2491 0.002756 4.922 5.415 5.894 1001 10000 beta[16] 5.921 0.2434 0.002616 5.451 5.92 6.402 1001 10000 beta[17] 6.273 0.2414 0.002537 5.801 6.273 6.755 1001 10000 beta[18] 5.845 0.243 0.00264 5.369 5.844 6.324 1001 10000 beta[19] 6.402 0.244 0.002438 5.929 6.402 6.882 1001 10000 beta[20] 6.055 0.238 0.002447 5.593 6.058 6.527 1001 10000 beta[21] 6.404 0.2415 0.002601 5.928 6.404 6.871 1001 10000 beta[22] 5.862 0.2421 0.002504 5.379 5.863 6.335 1001 10000 beta[23] 5.749 0.242 0.002603 5.267 5.75 6.221 1001 10000 beta[24] 5.889 0.241 0.002509 5.413 5.889 6.364 1001 10000 beta[25] 6.907 0.2538 0.002887 6.401 6.91 7.404 1001 10000 beta[26] 6.546 0.2387 0.002667 6.065 6.548 7.008 1001 10000 beta[27] 5.9 0.2421 0.002648 5.427 5.9 6.369 1001 10000 beta[28] 5.848 0.2445 0.002618 5.359 5.849 6.325 1001 10000 beta[29] 5.663 0.2442 0.0026 5.189 5.662 6.141 1001 10000 beta[30] 6.127 0.2402 0.002408 5.66 6.126 6.601 1001 10000 beta.c 6.185 0.1061 0.001313 5.975 6.185 6.395 1001 10000 mu[1,1] 155.0 4.361 0.04912 146.5 154.9 163.6 1001 10000 mu[1,2] 197.4 3.169 0.03588 191.2 197.4 203.7 1001 10000 mu[1,3] 239.9 2.671 0.02855 234.7 239.8 245.2 1001 10000 mu[1,4] 282.3 3.207 0.03157 276.1 282.3 288.6 1001 10000 mu[1,5] 324.8 4.415 0.04279 316.3 324.8 333.4 1001 10000 mu[2,1] 149.1 4.411 0.0494 140.4 149.1 157.8 1001 10000 mu[2,2] 198.5 3.175 0.03204 192.2 198.4 204.7 1001 10000 mu[2,3] 247.8 2.642 0.02543 242.6 247.8 253.0 1001 10000 mu[2,4] 297.1 3.189 0.03607 290.8 297.2 303.2 1001 10000 mu[2,5] 346.5 4.432 0.05468 337.6 346.5 355.1 1001 10000 mu[3,1] 161.7 4.34 0.04219 153.1 161.6 170.3 1001 10000 mu[3,2] 207.1 3.181 0.03043 200.8 207.1 213.3 1001 10000 mu[3,3] 252.4 2.677 0.02487 247.2 252.4 257.6 1001 10000 mu[3,4] 297.8 3.161 0.02928 291.7 297.8 304.1 1001 10000 mu[3,5] 343.2 4.311 0.04053 334.7 343.2 351.7 1001 10000 mu[4,1] 157.8 4.46 0.05048 149.0 157.8 166.4 1001 10000 mu[4,2] 195.2 3.215 0.03448 188.7 195.2 201.5 1001 10000 mu[4,3] 232.6 2.671 0.02729 227.3 232.6 237.8 1001 10000 mu[4,4] 270.0 3.206 0.03489 263.7 270.0 276.4 1001 10000 mu[4,5] 307.4 4.446 0.05104 298.7 307.4 316.3 1001 10000 mu[5,1] 139.7 4.366 0.04579 131.2 139.7 148.3 1001 10000 mu[5,2] 185.6 3.185 0.03017 179.4 185.6 192.0 1001 10000 mu[5,3] 231.6 2.677 0.02386 226.3 231.6 236.9 1001 10000 mu[5,4] 277.5 3.183 0.03278 271.2 277.6 283.7 1001 10000 mu[5,5] 323.5 4.364 0.04925 314.9 323.5 331.9 1001 10000 mu[6,1] 163.3 4.314 0.0439 154.8 163.3 171.6 1001 10000 mu[6,2] 206.5 3.168 0.03304 200.3 206.5 212.7 1001 10000 mu[6,3] 249.7 2.673 0.02963 244.4 249.8 255.0 1001 10000 mu[6,4] 293.0 3.151 0.03586 286.7 292.9 299.1 1001 10000 mu[6,5] 336.2 4.289 0.04813 327.6 336.1 344.8 1001 10000 mu[7,1] 145.0 4.307 0.04728 136.6 145.0 153.5 1001 10000 mu[7,2] 186.9 3.143 0.03511 180.8 186.9 193.0 1001 10000 mu[7,3] 228.7 2.647 0.02826 223.6 228.7 233.9 1001 10000 mu[7,4] 270.6 3.151 0.03055 264.4 270.6 276.7 1001 10000 mu[7,5] 312.4 4.32 0.04046 304.0 312.4 320.9 1001 10000 mu[8,1] 158.5 4.38 0.04657 149.9 158.5 167.3 1001 10000 mu[8,2] 203.4 3.202 0.0345 197.2 203.4 209.8 1001 10000 mu[8,3] 248.3 2.702 0.02836 243.1 248.4 253.6 1001 10000 mu[8,4] 293.3 3.214 0.0318 286.9 293.2 299.6 1001 10000 mu[8,5] 338.2 4.398 0.04256 329.5 338.1 346.9 1001 10000 mu[9,1] 184.7 4.379 0.0473 176.1 184.6 193.3 1001 10000 mu[9,2] 234.0 3.177 0.03243 227.8 234.0 240.1 1001 10000 mu[9,3] 283.3 2.704 0.02751 277.9 283.3 288.6 1001 10000 mu[9,4] 332.7 3.292 0.03677 326.0 332.7 339.0 1001 10000 mu[9,5] 382.0 4.545 0.05328 372.6 382.1 390.8 1001 10000 mu[10,1] 137.4 4.385 0.0486 128.8 137.4 146.1 1001 10000 mu[10,2] 178.4 3.208 0.03413 172.1 178.4 184.6 1001 10000 mu[10,3] 219.3 2.692 0.02606 214.1 219.3 224.6 1001 10000 mu[10,4] 260.2 3.179 0.03006 254.0 260.2 266.6 1001 10000 mu[10,5] 301.1 4.342 0.04289 292.7 301.1 309.8 1001 10000 mu[11,1] 163.1 4.411 0.05046 154.6 163.0 171.8 1001 10000 mu[11,2] 210.7 3.204 0.03569 204.5 210.6 217.1 1001 10000 mu[11,3] 258.2 2.677 0.02809 253.1 258.2 263.5 1001 10000 mu[11,4] 305.8 3.187 0.03303 299.6 305.8 312.0 1001 10000 mu[11,5] 353.4 4.386 0.04669 344.8 353.4 362.0 1001 10000 mu[12,1] 142.4 4.303 0.04779 133.9 142.5 151.0 1001 10000 mu[12,2] 185.3 3.173 0.03376 179.2 185.3 191.6 1001 10000 mu[12,3] 228.1 2.692 0.02707 223.0 228.2 233.4 1001 10000 mu[12,4] 271.0 3.169 0.03261 264.8 271.0 277.3 1001 10000 mu[12,5] 313.8 4.296 0.04617 305.4 313.8 322.2 1001 10000 mu[13,1] 156.1 4.342 0.04222 147.6 156.1 164.6 1001 10000 mu[13,2] 199.3 3.197 0.03134 193.1 199.3 205.5 1001 10000 mu[13,3] 242.4 2.693 0.02687 237.2 242.4 247.8 1001 10000 mu[13,4] 285.6 3.155 0.03166 279.4 285.6 291.8 1001 10000 mu[13,5] 328.8 4.281 0.04269 320.4 328.8 337.0 1001 10000 mu[14,1] 174.7 4.342 0.04496 166.2 174.7 183.2 1001 10000 mu[14,2] 221.5 3.173 0.03156 215.3 221.5 227.7 1001 10000 mu[14,3] 268.3 2.678 0.02649 263.0 268.3 273.5 1001 10000 mu[14,4] 315.1 3.189 0.03375 308.7 315.1 321.3 1001 10000 mu[14,5] 361.9 4.366 0.04803 353.2 361.9 370.3 1001 10000 mu[15,1] 166.9 4.397 0.04997 158.5 166.9 175.5 1001 10000 mu[15,2] 204.9 3.185 0.03528 198.7 204.9 211.1 1001 10000 mu[15,3] 242.8 2.651 0.02715 237.6 242.7 248.1 1001 10000 mu[15,4] 280.7 3.162 0.0312 274.6 280.6 286.9 1001 10000 mu[15,5] 318.6 4.364 0.04421 310.0 318.5 327.2 1001 10000 mu[16,1] 162.4 4.323 0.04542 153.9 162.5 170.8 1001 10000 mu[16,2] 203.9 3.169 0.0316 197.7 203.9 210.1 1001 10000 mu[16,3] 245.3 2.682 0.0246 240.1 245.3 250.6 1001 10000 mu[16,4] 286.8 3.187 0.0297 280.5 286.7 293.1 1001 10000 mu[16,5] 328.2 4.35 0.04277 319.7 328.2 336.8 1001 10000 mu[17,1] 144.4 4.312 0.04152 136.0 144.4 152.8 1001 10000 mu[17,2] 188.3 3.167 0.02932 182.1 188.3 194.6 1001 10000 mu[17,3] 232.2 2.679 0.02503 226.9 232.2 237.5 1001 10000 mu[17,4] 276.1 3.168 0.032 269.9 276.1 282.3 1001 10000 mu[17,5] 320.0 4.313 0.0453 311.5 320.0 328.5 1001 10000 mu[18,1] 158.6 4.301 0.04388 150.2 158.7 167.1 1001 10000 mu[18,2] 199.5 3.151 0.03076 193.3 199.5 205.7 1001 10000 mu[18,3] 240.5 2.672 0.02549 235.2 240.5 245.7 1001 10000 mu[18,4] 281.4 3.185 0.03219 275.1 281.4 287.6 1001 10000 mu[18,5] 322.3 4.351 0.04589 313.8 322.3 330.8 1001 10000 mu[19,1] 164.2 4.336 0.04267 155.6 164.2 172.7 1001 10000 mu[19,2] 209.0 3.177 0.02962 202.8 209.0 215.2 1001 10000 mu[19,3] 253.8 2.686 0.02272 248.5 253.8 259.1 1001 10000 mu[19,4] 298.6 3.189 0.02716 292.2 298.7 304.8 1001 10000 mu[19,5] 343.4 4.354 0.03926 334.9 343.5 352.0 1001 10000 mu[20,1] 156.9 4.28 0.04219 148.2 156.9 165.2 1001 10000 mu[20,2] 199.2 3.166 0.03077 192.9 199.3 205.5 1001 10000 mu[20,3] 241.6 2.698 0.02646 236.3 241.6 246.9 1001 10000 mu[20,4] 284.0 3.175 0.03226 277.8 284.0 290.2 1001 10000 mu[20,5] 326.4 4.294 0.04436 318.1 326.4 334.8 1001 10000 mu[21,1] 158.9 4.333 0.04633 150.5 158.9 167.5 1001 10000 mu[21,2] 203.8 3.191 0.03412 197.5 203.7 210.0 1001 10000 mu[21,3] 248.6 2.702 0.02906 243.2 248.6 253.8 1001 10000 mu[21,4] 293.4 3.185 0.03447 287.1 293.4 299.6 1001 10000 mu[21,5] 338.3 4.324 0.04685 329.8 338.2 346.7 1001 10000 mu[22,1] 143.2 4.34 0.04236 134.8 143.2 151.7 1001 10000 mu[22,2] 184.2 3.185 0.03075 178.0 184.2 190.4 1001 10000 mu[22,3] 225.3 2.684 0.02668 220.0 225.3 230.5 1001 10000 mu[22,4] 266.3 3.162 0.03305 260.0 266.3 272.5 1001 10000 mu[22,5] 307.3 4.306 0.04568 298.9 307.3 315.9 1001 10000 mu[23,1] 148.0 4.283 0.0455 139.6 147.9 156.5 1001 10000 mu[23,2] 188.2 3.145 0.03268 182.0 188.2 194.4 1001 10000 mu[23,3] 228.5 2.678 0.02701 223.2 228.5 233.8 1001 10000 mu[23,4] 268.7 3.193 0.03248 262.5 268.7 275.0 1001 10000 mu[23,5] 309.0 4.353 0.04522 300.5 309.0 317.4 1001 10000 mu[24,1] 162.7 4.334 0.04491 154.1 162.7 171.2 1001 10000 mu[24,2] 203.9 3.186 0.03425 197.7 203.9 210.1 1001 10000 mu[24,3] 245.1 2.683 0.03076 239.9 245.1 250.4 1001 10000 mu[24,4] 286.4 3.153 0.03655 280.1 286.4 292.6 1001 10000 mu[24,5] 327.6 4.287 0.04841 319.1 327.6 336.1 1001 10000 mu[25,1] 137.8 4.471 0.04483 129.1 137.7 146.6 1001 10000 mu[25,2] 186.1 3.244 0.03253 179.8 186.1 192.5 1001 10000 mu[25,3] 234.5 2.715 0.03038 229.2 234.5 239.8 1001 10000 mu[25,4] 282.8 3.245 0.04005 276.5 282.8 289.3 1001 10000 mu[25,5] 331.2 4.472 0.0557 322.4 331.2 340.0 1001 10000 mu[26,1] 162.4 4.266 0.0481 154.0 162.3 170.9 1001 10000 mu[26,2] 208.2 3.149 0.03494 202.0 208.2 214.4 1001 10000 mu[26,3] 254.0 2.685 0.02873 248.8 254.0 259.3 1001 10000 mu[26,4] 299.8 3.176 0.03358 293.5 299.8 306.0 1001 10000 mu[26,5] 345.6 4.306 0.04611 337.0 345.7 354.0 1001 10000 mu[27,1] 171.8 4.257 0.04695 163.4 171.8 180.0 1001 10000 mu[27,2] 213.1 3.111 0.03325 206.9 213.1 219.2 1001 10000 mu[27,3] 254.4 2.643 0.02636 249.2 254.4 259.5 1001 10000 mu[27,4] 295.7 3.168 0.03117 289.5 295.7 301.8 1001 10000 mu[27,5] 337.0 4.339 0.04399 328.4 337.0 345.2 1001 10000 mu[28,1] 161.1 4.349 0.0479 152.6 161.1 169.8 1001 10000 mu[28,2] 202.0 3.186 0.03492 195.7 202.0 208.4 1001 10000 mu[28,3] 243.0 2.692 0.02858 237.7 243.0 248.3 1001 10000 mu[28,4] 283.9 3.195 0.03295 277.6 283.9 290.2 1001 10000 mu[28,5] 324.9 4.362 0.04502 316.3 324.8 333.4 1001 10000 mu[29,1] 138.6 4.347 0.04565 130.1 138.6 147.3 1001 10000 mu[29,2] 178.3 3.191 0.03206 172.0 178.2 184.6 1001 10000 mu[29,3] 217.9 2.704 0.02519 212.6 217.9 223.2 1001 10000 mu[29,4] 257.5 3.207 0.03007 251.3 257.5 263.9 1001 10000 mu[29,5] 297.2 4.371 0.04285 288.6 297.1 305.7 1001 10000 mu[30,1] 155.7 4.35 0.04148 147.0 155.7 164.1 1001 10000 mu[30,2] 198.6 3.197 0.03095 192.3 198.6 204.8 1001 10000 mu[30,3] 241.4 2.679 0.02763 236.2 241.4 246.8 1001 10000 mu[30,4] 284.3 3.127 0.03373 278.2 284.3 290.5 1001 10000 mu[30,5] 327.2 4.247 0.04561 318.9 327.2 335.5 1001 10000 sigma 6.086 0.4606 0.007422 5.255 6.061 7.049 1001 10000 tau.alpha 0.004932 0.001367 1.492E-5 0.002688 0.004801 0.008 1001 10000 tau.beta 4.155 1.55 0.02774 1.95 3.888 7.911 1001 10000 tau.c 0.02746 0.004124 6.667E-5 0.02013 0.02723 0.03625 1001 10000
Node statistics node mean sd MC error 2.5% median 97.5% start sample alpha[1] 239.9 2.709 0.02984 234.5 239.9 245.2 1001 10000 alpha[2] 247.8 2.702 0.02425 242.6 247.8 253.1 1001 10000 alpha[3] 252.4 2.659 0.0213 247.3 252.5 257.7 1001 10000 alpha[4] 232.5 2.679 0.02458 227.3 232.6 237.7 1001 10000 alpha[5] 231.7 2.663 0.02514 226.4 231.7 236.9 1001 10000 alpha[6] 249.8 2.65 0.02415 244.6 249.8 255.0 1001 10000 alpha[7] 228.7 2.646 0.02366 223.5 228.7 233.9 1001 10000 alpha[8] 248.4 2.704 0.02569 243.1 248.4 253.6 1001 10000 alpha[9] 283.4 2.706 0.02924 278.1 283.4 288.7 1001 10000 alpha[10] 219.2 2.681 0.02928 214.0 219.2 224.5 1001 10000 alpha[11] 258.3 2.673 0.02572 252.9 258.3 263.4 1001 10000 alpha[12] 228.1 2.686 0.02537 222.8 228.1 233.5 1001 10000 alpha[13] 242.4 2.667 0.0287 237.1 242.4 247.5 1001 10000 alpha[14] 268.3 2.707 0.02451 262.9 268.3 273.6 1001 10000 alpha[15] 242.8 2.681 0.02934 237.5 242.8 248.1 1001 10000 alpha[16] 245.4 2.682 0.02593 240.0 245.4 250.5 1001 10000 alpha[17] 232.2 2.668 0.03022 227.0 232.2 237.4 1001 10000 alpha[18] 240.5 2.683 0.02907 235.2 240.5 245.8 1001 10000 alpha[19] 253.8 2.667 0.02977 248.6 253.7 259.1 1001 10000 alpha[20] 241.6 2.702 0.02906 236.3 241.6 246.9 1001 10000 alpha[21] 248.6 2.663 0.02487 243.2 248.6 253.7 1001 10000 alpha[22] 225.3 2.689 0.02645 220.0 225.2 230.6 1001 10000 alpha[23] 228.5 2.654 0.02464 223.3 228.5 233.7 1001 10000 alpha[24] 245.1 2.668 0.02811 239.9 245.1 250.4 1001 10000 alpha[25] 234.5 2.67 0.02429 229.2 234.5 239.7 1001 10000 alpha[26] 254.0 2.726 0.0283 248.6 254.0 259.2 1001 10000 alpha[27] 254.4 2.684 0.02426 249.1 254.4 259.6 1001 10000 alpha[28] 243.0 2.659 0.02653 237.8 243.0 248.2 1001 10000 alpha[29] 217.9 2.699 0.02643 212.6 217.9 223.2 1001 10000 alpha[30] 241.4 2.683 0.02469 236.1 241.4 246.6 1001 10000 alpha.c 242.6 2.78 0.02816 237.3 242.6 248.2 1001 10000 alpha0 106.6 3.65 0.04151 99.43 106.5 113.9 1001 10000 beta[1] 6.06 0.244 0.002281 5.587 6.056 6.54 1001 10000 beta[2] 7.068 0.2513 0.002792 6.564 7.067 7.552 1001 10000 beta[3] 6.485 0.242 0.002477 6.013 6.484 6.97 1001 10000 beta[4] 5.333 0.2554 0.002823 4.832 5.333 5.837 1001 10000 beta[5] 6.576 0.244 0.002394 6.102 6.574 7.059 1001 10000 beta[6] 6.174 0.2439 0.002296 5.695 6.174 6.658 1001 10000 beta[7] 5.98 0.2432 0.002558 5.503 5.98 6.456 1001 10000 beta[8] 6.42 0.245 0.002323 5.942 6.42 6.896 1001 10000 beta[9] 7.064 0.255 0.003149 6.562 7.064 7.567 1001 10000 beta[10] 5.846 0.2425 0.002341 5.363 5.847 6.319 1001 10000 beta[11] 6.806 0.2464 0.002708 6.32 6.808 7.282 1001 10000 beta[12] 6.118 0.2409 0.002511 5.65 6.115 6.601 1001 10000 beta[13] 6.159 0.2423 0.002466 5.673 6.158 6.628 1001 10000 beta[14] 6.696 0.2462 0.002467 6.211 6.694 7.186 1001 10000 beta[15] 5.407 0.2558 0.002956 4.917 5.406 5.914 1001 10000 beta[16] 5.919 0.2442 0.002639 5.436 5.919 6.397 1001 10000 beta[17] 6.274 0.2456 0.002604 5.785 6.278 6.755 1001 10000 beta[18] 5.841 0.2439 0.002864 5.364 5.843 6.316 1001 10000 beta[19] 6.407 0.2402 0.002522 5.94 6.404 6.887 1001 10000 beta[20] 6.051 0.2429 0.002321 5.582 6.052 6.52 1001 10000 beta[21] 6.41 0.2393 0.002444 5.945 6.412 6.881 1001 10000 beta[22] 5.85 0.2474 0.002406 5.366 5.852 6.332 1001 10000 beta[23] 5.736 0.2489 0.002605 5.245 5.738 6.223 1001 10000 beta[24] 5.885 0.2411 0.002232 5.403 5.886 6.351 1001 10000 beta[25] 6.918 0.2543 0.003034 6.413 6.918 7.414 1001 10000 beta[26] 6.554 0.2443 0.002606 6.078 6.552 7.033 1001 10000 beta[27] 5.893 0.2436 0.002648 5.418 5.889 6.378 1001 10000 beta[28] 5.842 0.2425 0.00244 5.364 5.844 6.32 1001 10000 beta[29] 5.664 0.2487 0.002759 5.178 5.664 6.147 1001 10000 beta[30] 6.132 0.243 0.00257 5.65 6.131 6.608 1001 10000 beta.c 6.185 0.1102 0.001294 5.967 6.185 6.404 1001 10000 mu[1,1] 155.1 4.341 0.04037 146.5 155.1 163.5 1001 10000 mu[1,2] 197.5 3.19 0.0317 191.2 197.5 203.8 1001 10000 mu[1,3] 239.9 2.709 0.02984 234.5 239.9 245.2 1001 10000 mu[1,4] 282.3 3.214 0.03585 276.0 282.3 288.6 1001 10000 mu[1,5] 324.7 4.377 0.0468 316.3 324.7 333.3 1001 10000 mu[2,1] 148.9 4.462 0.0433 140.1 148.8 157.7 1001 10000 mu[2,2] 198.3 3.242 0.02915 192.1 198.3 204.7 1001 10000 mu[2,3] 247.8 2.702 0.02425 242.6 247.8 253.1 1001 10000 mu[2,4] 297.3 3.207 0.03302 290.9 297.3 303.5 1001 10000 mu[2,5] 346.8 4.411 0.04854 338.0 346.8 355.4 1001 10000 mu[3,1] 161.6 4.259 0.04094 153.3 161.6 169.9 1001 10000 mu[3,2] 207.0 3.12 0.02765 200.9 207.0 213.2 1001 10000 mu[3,3] 252.4 2.659 0.0213 247.3 252.5 257.7 1001 10000 mu[3,4] 297.8 3.186 0.02729 291.6 297.8 304.0 1001 10000 mu[3,5] 343.2 4.355 0.04046 334.7 343.3 351.8 1001 10000 mu[4,1] 157.9 4.461 0.0459 149.2 157.9 166.7 1001 10000 mu[4,2] 195.2 3.216 0.03106 188.8 195.3 201.5 1001 10000 mu[4,3] 232.5 2.679 0.02458 227.3 232.6 237.7 1001 10000 mu[4,4] 269.9 3.226 0.03201 263.6 269.9 276.2 1001 10000 mu[4,5] 307.2 4.476 0.04718 298.6 307.2 316.1 1001 10000 mu[5,1] 139.6 4.332 0.04097 131.2 139.6 148.4 1001 10000 mu[5,2] 185.6 3.164 0.02957 179.5 185.6 192.0 1001 10000 mu[5,3] 231.7 2.663 0.02514 226.4 231.7 236.9 1001 10000 mu[5,4] 277.7 3.163 0.03085 271.5 277.7 283.9 1001 10000 mu[5,5] 323.7 4.33 0.04281 315.3 323.7 332.4 1001 10000 mu[6,1] 163.4 4.331 0.03925 154.9 163.4 171.7 1001 10000 mu[6,2] 206.6 3.158 0.02835 200.4 206.6 212.7 1001 10000 mu[6,3] 249.8 2.65 0.02415 244.6 249.8 255.0 1001 10000 mu[6,4] 293.0 3.147 0.02965 286.8 293.0 299.2 1001 10000 mu[6,5] 336.2 4.314 0.04112 327.8 336.2 344.7 1001 10000 mu[7,1] 145.0 4.319 0.04387 136.6 145.0 153.6 1001 10000 mu[7,2] 186.8 3.151 0.03035 180.8 186.8 193.0 1001 10000 mu[7,3] 228.7 2.646 0.02366 223.5 228.7 233.9 1001 10000 mu[7,4] 270.5 3.142 0.02897 264.4 270.5 276.7 1001 10000 mu[7,5] 312.4 4.306 0.04196 304.0 312.4 320.8 1001 10000 mu[8,1] 158.5 4.365 0.04066 149.9 158.5 167.0 1001 10000 mu[8,2] 203.5 3.2 0.02987 197.2 203.5 209.8 1001 10000 mu[8,3] 248.4 2.704 0.02569 243.1 248.4 253.6 1001 10000 mu[8,4] 293.3 3.205 0.03093 287.0 293.4 299.5 1001 10000 mu[8,5] 338.3 4.372 0.04221 329.7 338.3 346.7 1001 10000 mu[9,1] 184.5 4.437 0.05666 175.8 184.4 193.1 1001 10000 mu[9,2] 233.9 3.212 0.03933 227.7 233.9 240.2 1001 10000 mu[9,3] 283.4 2.706 0.02924 278.1 283.4 288.7 1001 10000 mu[9,4] 332.8 3.27 0.03369 326.3 332.8 339.2 1001 10000 mu[9,5] 382.3 4.521 0.04885 373.2 382.3 391.2 1001 10000 mu[10,1] 137.4 4.297 0.04316 128.9 137.4 145.9 1001 10000 mu[10,2] 178.3 3.153 0.03304 172.2 178.3 184.5 1001 10000 mu[10,3] 219.2 2.681 0.02928 214.0 219.2 224.5 1001 10000 mu[10,4] 260.1 3.193 0.03406 253.9 260.1 266.4 1001 10000 mu[10,5] 301.0 4.355 0.04472 292.6 301.0 309.7 1001 10000 mu[11,1] 163.0 4.348 0.04726 154.5 163.0 171.5 1001 10000 mu[11,2] 210.6 3.17 0.03299 204.4 210.6 216.8 1001 10000 mu[11,3] 258.3 2.673 0.02572 252.9 258.3 263.4 1001 10000 mu[11,4] 305.9 3.192 0.03088 299.4 305.9 312.0 1001 10000 mu[11,5] 353.5 4.38 0.04432 344.7 353.6 362.0 1001 10000 mu[12,1] 142.4 4.323 0.04469 133.8 142.5 150.9 1001 10000 mu[12,2] 185.2 3.179 0.03181 179.0 185.3 191.5 1001 10000 mu[12,3] 228.1 2.686 0.02537 222.8 228.1 233.5 1001 10000 mu[12,4] 270.9 3.163 0.0299 264.8 270.9 277.2 1001 10000 mu[12,5] 313.7 4.3 0.04198 305.4 313.7 322.1 1001 10000 mu[13,1] 156.2 4.322 0.04484 147.6 156.2 164.5 1001 10000 mu[13,2] 199.3 3.166 0.03345 193.0 199.3 205.4 1001 10000 mu[13,3] 242.4 2.667 0.0287 237.1 242.4 247.5 1001 10000 mu[13,4] 285.5 3.155 0.03354 279.2 285.5 291.6 1001 10000 mu[13,5] 328.6 4.307 0.04496 320.1 328.6 336.9 1001 10000 mu[14,1] 174.6 4.371 0.04435 166.1 174.5 183.2 1001 10000 mu[14,2] 221.4 3.201 0.03139 215.2 221.4 227.8 1001 10000 mu[14,3] 268.3 2.707 0.02451 262.9 268.3 273.6 1001 10000 mu[14,4] 315.2 3.217 0.0285 308.9 315.2 321.4 1001 10000 mu[14,5] 362.0 4.395 0.04026 353.6 362.0 370.7 1001 10000 mu[15,1] 167.1 4.431 0.04947 158.2 167.1 175.7 1001 10000 mu[15,2] 204.9 3.194 0.03501 198.6 205.0 211.2 1001 10000 mu[15,3] 242.8 2.681 0.02934 237.5 242.8 248.1 1001 10000 mu[15,4] 280.6 3.253 0.03677 274.4 280.6 287.0 1001 10000 mu[15,5] 318.5 4.515 0.05196 309.7 318.5 327.5 1001 10000 mu[16,1] 162.5 4.337 0.0402 154.0 162.5 171.0 1001 10000 mu[16,2] 203.9 3.175 0.02834 197.8 203.9 210.1 1001 10000 mu[16,3] 245.4 2.682 0.02593 240.0 245.4 250.5 1001 10000 mu[16,4] 286.8 3.185 0.03499 280.5 286.8 292.9 1001 10000 mu[16,5] 328.2 4.352 0.04959 319.7 328.3 336.6 1001 10000 mu[17,1] 144.3 4.385 0.04819 135.7 144.3 152.9 1001 10000 mu[17,2] 188.3 3.196 0.03586 182.0 188.3 194.5 1001 10000 mu[17,3] 232.2 2.668 0.03022 227.0 232.2 237.4 1001 10000 mu[17,4] 276.1 3.152 0.03473 269.9 276.1 282.3 1001 10000 mu[17,5] 320.0 4.32 0.0465 311.5 320.0 328.4 1001 10000 mu[18,1] 158.7 4.3 0.04975 150.1 158.8 167.1 1001 10000 mu[18,2] 199.6 3.151 0.03547 193.4 199.7 205.7 1001 10000 mu[18,3] 240.5 2.683 0.02907 235.2 240.5 245.8 1001 10000 mu[18,4] 281.4 3.208 0.03515 275.2 281.3 287.7 1001 10000 mu[18,5] 322.2 4.384 0.0493 313.6 322.2 330.9 1001 10000 mu[19,1] 164.1 4.281 0.04736 155.6 164.1 172.3 1001 10000 mu[19,2] 208.9 3.145 0.0354 202.7 208.9 215.1 1001 10000 mu[19,3] 253.8 2.667 0.02977 248.6 253.7 259.1 1001 10000 mu[19,4] 298.6 3.16 0.03381 292.4 298.6 304.8 1001 10000 mu[19,5] 343.5 4.303 0.04498 335.1 343.5 351.9 1001 10000 mu[20,1] 156.9 4.369 0.0468 148.4 156.9 165.3 1001 10000 mu[20,2] 199.2 3.209 0.0354 193.0 199.3 205.5 1001 10000 mu[20,3] 241.6 2.702 0.02906 236.3 241.6 246.9 1001 10000 mu[20,4] 284.0 3.175 0.03104 277.7 283.9 290.2 1001 10000 mu[20,5] 326.3 4.318 0.04014 317.8 326.3 334.7 1001 10000 mu[21,1] 158.8 4.298 0.0374 150.6 158.8 167.4 1001 10000 mu[21,2] 203.7 3.158 0.02675 197.5 203.7 209.9 1001 10000 mu[21,3] 248.6 2.663 0.02487 243.2 248.6 253.7 1001 10000 mu[21,4] 293.5 3.134 0.03327 287.3 293.5 299.6 1001 10000 mu[21,5] 338.3 4.263 0.0467 329.9 338.3 346.6 1001 10000 mu[22,1] 143.4 4.37 0.04641 134.7 143.4 151.9 1001 10000 mu[22,2] 184.3 3.188 0.03381 178.1 184.3 190.6 1001 10000 mu[22,3] 225.3 2.689 0.02645 220.0 225.2 230.6 1001 10000 mu[22,4] 266.2 3.208 0.0287 259.9 266.2 272.6 1001 10000 mu[22,5] 307.2 4.4 0.03892 298.4 307.2 315.9 1001 10000 mu[23,1] 148.2 4.344 0.04298 139.6 148.1 156.8 1001 10000 mu[23,2] 188.3 3.15 0.02991 182.0 188.3 194.5 1001 10000 mu[23,3] 228.5 2.654 0.02464 223.3 228.5 233.7 1001 10000 mu[23,4] 268.6 3.199 0.03137 262.4 268.6 274.9 1001 10000 mu[23,5] 308.8 4.416 0.04502 300.1 308.8 317.5 1001 10000 mu[24,1] 162.7 4.261 0.03874 154.3 162.7 171.1 1001 10000 mu[24,2] 203.9 3.129 0.03002 197.7 203.9 210.0 1001 10000 mu[24,3] 245.1 2.668 0.02811 239.9 245.1 250.4 1001 10000 mu[24,4] 286.3 3.185 0.03416 280.0 286.3 292.6 1001 10000 mu[24,5] 327.5 4.344 0.04508 318.9 327.5 335.9 1001 10000 mu[25,1] 137.6 4.47 0.04839 128.8 137.6 146.6 1001 10000 mu[25,2] 186.0 3.223 0.03186 179.7 186.0 192.5 1001 10000 mu[25,3] 234.5 2.67 0.02429 229.2 234.5 239.7 1001 10000 mu[25,4] 282.9 3.195 0.03267 276.6 282.9 289.1 1001 10000 mu[25,5] 331.3 4.43 0.04946 322.7 331.3 340.0 1001 10000 mu[26,1] 162.2 4.358 0.04652 153.7 162.2 170.7 1001 10000 mu[26,2] 208.1 3.207 0.03391 201.8 208.1 214.4 1001 10000 mu[26,3] 254.0 2.726 0.0283 248.6 254.0 259.2 1001 10000 mu[26,4] 299.9 3.228 0.03344 293.4 299.9 306.1 1001 10000 mu[26,5] 345.7 4.389 0.04584 336.9 345.8 354.2 1001 10000 mu[27,1] 171.9 4.368 0.04558 163.2 172.0 180.5 1001 10000 mu[27,2] 213.2 3.199 0.03145 206.9 213.2 219.4 1001 10000 mu[27,3] 254.4 2.684 0.02426 249.1 254.4 259.6 1001 10000 mu[27,4] 295.7 3.16 0.02958 289.5 295.7 301.9 1001 10000 mu[27,5] 336.9 4.31 0.04299 328.5 336.9 345.4 1001 10000 mu[28,1] 161.2 4.292 0.04433 152.7 161.3 169.5 1001 10000 mu[28,2] 202.1 3.141 0.03229 195.9 202.2 208.3 1001 10000 mu[28,3] 243.0 2.659 0.02653 237.8 243.0 248.2 1001 10000 mu[28,4] 283.9 3.168 0.0308 277.7 283.9 290.2 1001 10000 mu[28,5] 324.8 4.332 0.04216 316.5 324.8 333.2 1001 10000 mu[29,1] 138.6 4.397 0.04733 129.9 138.5 147.1 1001 10000 mu[29,2] 178.2 3.206 0.03311 171.9 178.2 184.5 1001 10000 mu[29,3] 217.9 2.699 0.02643 212.6 217.9 223.2 1001 10000 mu[29,4] 257.5 3.217 0.03236 251.3 257.5 263.8 1001 10000 mu[29,5] 297.2 4.413 0.04628 288.5 297.1 305.8 1001 10000 mu[30,1] 155.6 4.376 0.04098 146.9 155.6 164.2 1001 10000 mu[30,2] 198.5 3.206 0.02865 192.2 198.5 204.8 1001 10000 mu[30,3] 241.4 2.683 0.02469 236.1 241.4 246.6 1001 10000 mu[30,4] 284.3 3.147 0.03233 278.1 284.4 290.4 1001 10000 mu[30,5] 327.3 4.288 0.04613 318.8 327.3 335.6 1001 10000 sigma 6.074 0.4673 0.007724 5.247 6.044 7.068 1001 10000 sigma.alpha 14.88 2.135 0.02675 11.28 14.64 19.72 1001 10000 sigma.beta 0.5317 0.09454 0.001509 0.3679 0.5237 0.7416 1001 10000 tau.alpha 0.004791 0.001334 1.517E-5 0.002573 0.004666 0.007854 1001 10000 tau.beta 3.884 1.423 0.02366 1.82 3.646 7.389 1001 10000 tau.c 0.02758 0.004191 6.869E-5 0.02002 0.02737 0.03633 1001 10000Comparing the above two sets of results node by node is inconvenient, because one must constantly switch which file one is viewing, and each time search for the same node within two different files. Summarizing all nodes from both runs together within an Html table provides one solution to this problem.
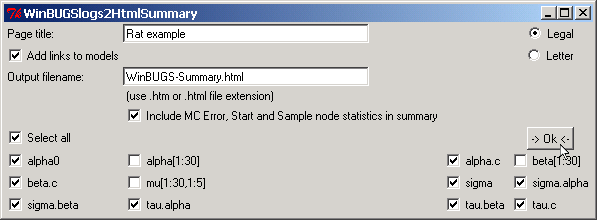
| Here are the steps in running WinBUGSLogs2HtmlSummary: First, from Windows Explorer, drag-and-drop the two (can be more than two, but in this example we have only two) WinBUGS text log files onto WinBUGSLogs2HtmlSummary's Desktop Icon. A form then pops up (right). |
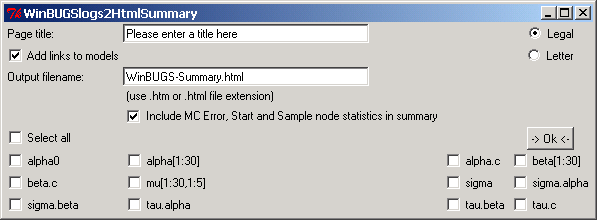 |
| Enter a relevant title in the title box. |
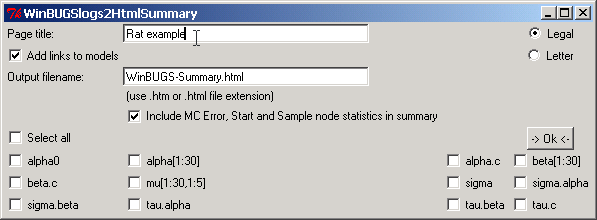 |
| Since we want to compare Node Statistics for almost all nodes listed, we will first select all of them by clicking the tick box next to Select all |
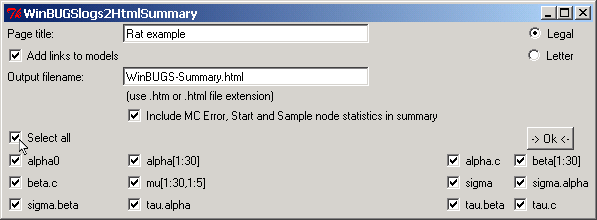 |
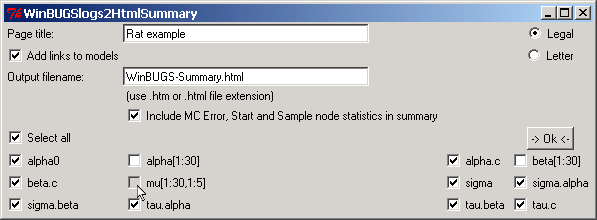
| For illustrative purposes, we will unselect the nodes alpha, beta and mu (you might of course be interested in these comparisons also) by unticking the appropriate boxes. |
 |
|
For more concise outputs, one may prefer to exclude MC Error, Start and Sample Node Statistics from the summary by by unticking the box below the filename window. When the Start and Sample Node Statistics are the same for each node in every log file, their values are automatically relegated to the narrower bottom section of the output summary, along with WinBUGS log file names and paths. The upper corner radio button allows you to chose Legal or Letter format, which can be useful even if you do not intend to print the summary. Indeed, this option allows you to select the maximal width of the output summary: Legal will fit on a 8½ in x 14 in sheet (landscape) while Letter will fit (landscape) on a 8½ in x 11 in sheet. Finally, the upper-left corner tick box allows you to add links to models; in doing so, the WinBUGS log file names, when clicked, will open the file with model used in the corresponding script. This, however, comes with a warning: indeed, the link is to the model file given on the check() WinBUGS script command, but this file may have changed since the log file was produced (if you consult the summary days or weeks later), thus it may not correspond to the actual model used to produce the results presented in the summary. | |
| Click Ok button to submit. |
 |
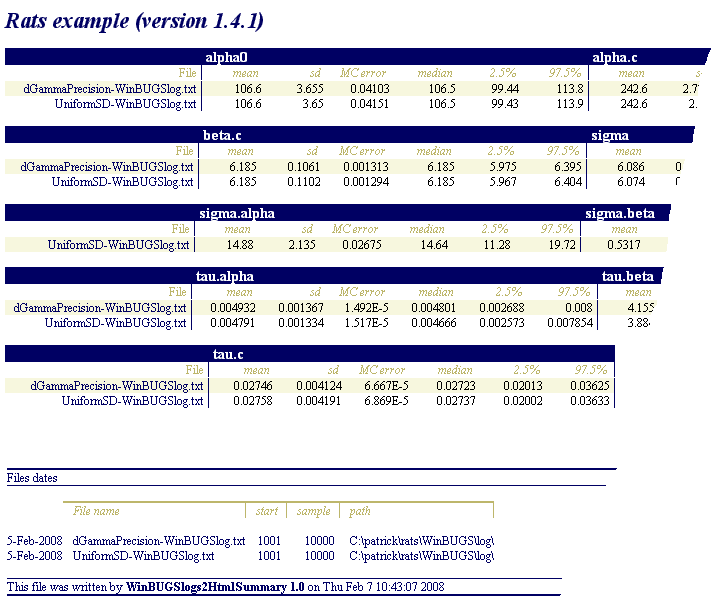
In the example above, the summary will be saved to file WinBUGS-summary.html, which will resemble (click image to see actual summary file):
Top
Download WinBUGSLogs2HtmlSummary
WinBUGSLogs2HtmlSummary is a free program. Save and unzip version 1.8 under the name WinBUGSLogs2HtmlSummary.pl and read the section below.
WinBUGSLogs2HtmlSummary also needs Tkx Perl module be installed. Read Perl package manager instructions on how to install Tkx in a few clicks.
Top
How to use WinBUGSLogs2HtmlSummary
WinBUGSLogs2HtmlSummary is a program written in Perl. Please refer to my generic page on running Perl programs for instructions.
Top
Details of example above
The example used in this document is the Rats example, originally presented in WinBUGS examples manual, version 1.4.1. We reproduce below the two models used, the data set and the two sets of initial values used to obtain the results presented above.
Model 1 (uniform distribution on SD)
# UniformSD
model
{
for( i in 1 : N )
{
for( j in 1 : T )
{
Y[i , j] ~ dnorm(mu[i , j],tau.c)
mu[i , j] <- alpha[i] + beta[i] * (x[j] - xbar)
}
alpha[i] ~ dnorm(alpha.c, tau.alpha)
beta[i] ~ dnorm(beta.c, tau.beta)
}
tau.c ~ dgamma(0.001,0.001)
sigma <- 1 / sqrt(tau.c)
alpha.c ~ dnorm(0.0,1.0E-6)
beta.c ~ dnorm(0.0,1.0E-6)
alpha0 <- alpha.c - xbar * beta.c
# Choice of prior of random effects variances
# Prior: uniform on SD
sigma.alpha ~ dunif(0,100)
sigma.beta ~ dunif(0,100)
tau.alpha <- 1/(sigma.alpha*sigma.alpha)
tau.beta <- 1/(sigma.beta*sigma.beta)
}
Model 2 (dgamma on precision [not recommanded])
# dGammaPrecision
model
{
for( i in 1 : N )
{
for( j in 1 : T )
{
Y[i , j] ~ dnorm(mu[i , j],tau.c)
mu[i , j] <- alpha[i] + beta[i] * (x[j] - xbar)
}
alpha[i] ~ dnorm(alpha.c, tau.alpha)
beta[i] ~ dnorm(beta.c, tau.beta)
}
tau.c ~ dgamma(0.001,0.001)
sigma <- 1 / sqrt(tau.c)
alpha.c ~ dnorm(0.0,1.0E-6)
beta.c ~ dnorm(0.0,1.0E-6)
alpha0 <- alpha.c - xbar * beta.c
# Prior: dgamma on precision (not recommended)
tau.alpha ~ dgamma(0.001,0.001)
tau.beta ~ dgamma(0.001,0.001)
}
The data to analyze are those presented in the following WinBUGS list
list(x = c(8.0, 15.0, 22.0, 29.0, 36.0), xbar = 22, N = 30, T = 5,
Y = structure(
.Data = c(151, 199, 246, 283, 320,
145, 199, 249, 293, 354,
147, 214, 263, 312, 328,
155, 200, 237, 272, 297,
135, 188, 230, 280, 323,
159, 210, 252, 298, 331,
141, 189, 231, 275, 305,
159, 201, 248, 297, 338,
177, 236, 285, 350, 376,
134, 182, 220, 260, 296,
160, 208, 261, 313, 352,
143, 188, 220, 273, 314,
154, 200, 244, 289, 325,
171, 221, 270, 326, 358,
163, 216, 242, 281, 312,
160, 207, 248, 288, 324,
142, 187, 234, 280, 316,
156, 203, 243, 283, 317,
157, 212, 259, 307, 336,
152, 203, 246, 286, 321,
154, 205, 253, 298, 334,
139, 190, 225, 267, 302,
146, 191, 229, 272, 302,
157, 211, 250, 285, 323,
132, 185, 237, 286, 331,
160, 207, 257, 303, 345,
169, 216, 261, 295, 333,
157, 205, 248, 289, 316,
137, 180, 219, 258, 291,
153, 200, 244, 286, 324),
.Dim = c(30,5)))
while the set of initial values used for Model 1 was
list(alpha = c(250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250,
250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250),
beta = c(6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6,
6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6),
alpha.c = 150, beta.c = 10,
tau.c = 1, sigma.alpha = 1, sigma.beta = 1)
and the set of initial values used for Model 2 was
list(alpha = c(250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250,
250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250, 250),
beta = c(6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6,
6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6),
alpha.c = 150, beta.c = 10,
tau.c = 1, tau.alpha = 1, tau.beta = 1)