|
RMP
Laboratory |
RMP >
Theory Nernst
Equation |
| |
The value of the equilibrium potential for any ion depends
upon the concentration gradient for that ion across the membrane. If the concentrations on
the two sides were equal, the force of the concentration gradient would be zero, and the
equilibrium potential would also be zero. The larger the concentration gradient, the
larger is the equilibrium potential. The equilibrium potential for any ion can be
calculated using the so called Nernst equation. |
| |
|
| In this experiment, we will test the
hypothesis that the muscle membrane at
rest is exclusively permeable to potassium. If this hypothesis is valid, then the
resting membrane potential should be the same as the equilibrium potential for potassium. Hypothesis: Em = Ek |
| Therefore it should be possible to predict the changes in resting membrane potential for
various [K+]o using
simply the Nernst equation which for potassium ions is : |
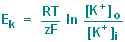 |
R = gas constant (8.31
joule/degree Kelvin-mole)
T = absolute temperature (degrees Kelvin)
F = Faraday constant (9.65 x 10^4 coulomb/mole)
z = the valence of the ion, in this case 1
[K+]o = extracellular K concentration in mM
[K+]i = intracellular K concentration in mM
ln = logarithm with base e |
| At room
temperature, this equation can be reduced to:

|
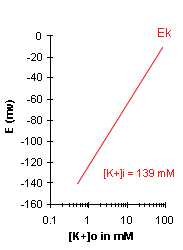
| A graph of Ek vs log10[K+]o
will be a straight line with a slope of 58. Note that for a 10-fold change in [K+]o, Ek
will change by 58 mV. For a 100-fold change in [K+]o, Ek will change by 116 mV (58 + 58).
In the box below, you can enter sample [K+]o values and Ek will be calculated for
you. For physiological conditions, we will assume that [K+]i = 139 mM. In the graph to the
right, Ek is plotted, assuming that a [K+]i of 139mM remains the same as [K+]o changes. In
the graph, note the general trend of the Ek: with increasing [K+]o, Ek is reduced, i.e.
becomes less negative. |
|
|
 |
|
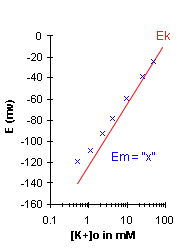
If Em=Ek, then the graph for Em should appear
similar to that for Ek as given above. However as you will see after performing the lab,
this is not the case. At physiological
levels of [K+], the measured membrane potential is usually less negative than the
potassium equilibrium potential (Ek), mainly because the Na+ permeability although small,
is not zero at rest. Thus we will conclude that although Em is close to Ek, it is not
exactly equal; especially at low [K+]o, due to the influence of Na+.
|
 |
|
The influence of other ions
is best determined using the Goldman
Equation, which is similar in form to the Nernst Equation, but incorporates
permeability to Na and Cl. (In fact, the inclusion of Cl does not appreciably affect the
solution of the equation.) |
|
Goldman Equation
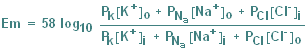 |
|
To continue to the next section: Recording Circuit, click here |